The Eight Queens Puzzle
This article covers recursion with backtracking approach to solving the eight queens problem. This article is self-contained. However, familiarity and exposure to recursion would be helpful.
“Knowledge is limited. Imagination encircles the world.”
–Albert Einstein
The Problem Statement
Assume an 8x8 chess board and eight queens. Our task is to place all of the eight queens such that none of the queens threaten each other—that is there is no other queen in the same row, column, rising diagonal, and falling diagonal. The task is to find all such configurations of queens on the 8x8 board. There are 92 possible configurations.
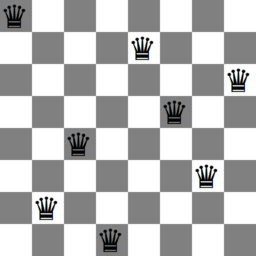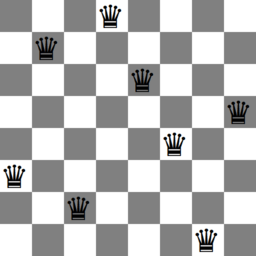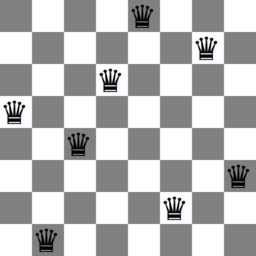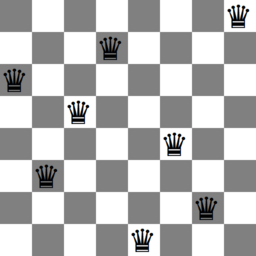
figure 1: An animation of all solutions to the eight queens problem.
The N-Queens version (generalized case)
The generalization considers an nxn board with n queens. The problem statement is the same as the previous eight queens problem with the same constraints for n queens on n x n board.
Number of Solutions
As of the time of this writing, there is no known formula to determine the number of solutions to the general n-queens problem. We currently know the number of solutions to boards up to size n = 27. If you are wondering, a 27 x 27 board has a staggering 234,907,967,154,122,528 solutions. No doubt a full list of solutions for larger n would be found in the near future, but unless there is a radical fundamental understanding or discovery made about such problems, do not hold out for solutions for even modest sizes of n.1 2
A paper by Zur Luria titled New bounds on the number of n-queens configurations goes into more detail on estimated number of solutions for the toroidal version of this problem. Interestingly, there has been recent activity on this topic. Resources are below:
- Simkin, Michael. “The number of $n$-queens configurations”. arXiv:2107.13460v2
- Sloman, Leila. “Mathematician Answers Chess Problem About Attacking Queens”.
- Luria, Zur. “New bounds on the number of n-queens configurations”. arXiv:1705.05225v2.
- Bowtell, Candida; Keevash, Peter. “The $n$-queens problem”. arXiv:2109.08083v1.
Warm up example
Before we jump to an 8x8 board, let us briefly consider a 4x4 board as an exercise. We can place four queens on this board. Can you find a solution? Take some time to play around with it. Take a piece of paper and draw a grid to fit 16 cells in 4x4 arrangement.
The first queen is placed in the right spot for you to get started. You are solving a variation of the problem called the N-Queens completion problem. A good question to ask is does it matter if the initial queen placement or placements were correct or not in regards to the difficulty of the problem?
Your task is to fill in the remaining three queens. Remember no queen can threaten another along the horizontal, vertical, or both diagonals. Take your time.
Click/Tap the image below for the solution

figure 2: A 4x4 board with a placed queen
Proceed when done. Click/Tap the image above to reveal the solution.
Congratulations
Reveal Spoiler (How many total solutions are there for a 4x4 board?)
There are only two 4 x 4 solutions.
Below is a decision tree on how to place the queens:
Reveal Spoiler (Decision Tree)
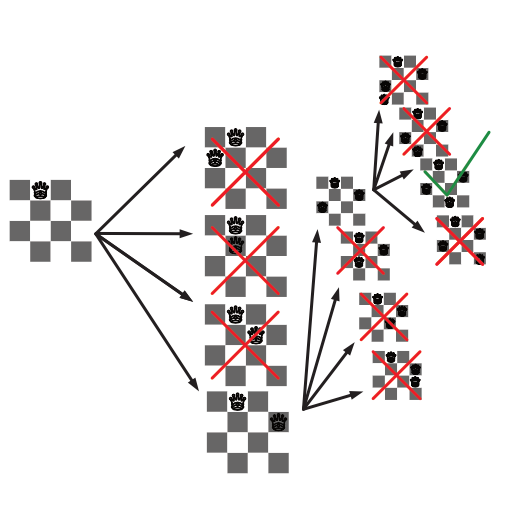
figure 3: Partial decision tree for 4x4 board above
Reveal Spoiler (Solution 1)

figure 4: 4-Queens Solution # 1
Reveal Spoiler (Solution 2)

figure 5: 4-Queens Solution # 2
Before moving on, as an exercise how many solutions are there for a board size of 1 x 1, 2 x 2, and 3 x 3?
Reveal Spoiler (Answer)
one, zero, zero.
The way you can confirm this is by counting, and since the case is small enough, it can be done by hand. What you do is systematically enumerate all possible configurations until you exhaust all of them. Record only the legal ones. For the case of one queen on 1x1, board it is trivial. For the case 2x2, it is easy enough to see that no matter where a queen is placed, the remaining spots are threatened. There is no way to place a second queen without it being threatened. A 3x3 case is very similar to a 2x2 case. Try it out.

figure 6: A board of size 1x1

figure 7: A board of size 2x2

figure 8: A board of size 3x3
The list of currently know solutions as a function of board size (n x n):
| n | Solutions(n) |
|---|---|
| 1 | 1 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 2 |
| 6 | 1 |
| 7 | 6 |
| 8 | 12 |
| 9 | 46 |
| 10 | 92 |
| 11 | 341 |
| 12 | 1787 |
| 13 | 9233 |
| 14 | 45752 |
| 15 | 285053 |
| 16 | 1846955 |
| 17 | 11977939 |
| 18 | 83263591 |
| 19 | 621012754 |
| 20 | 4878666808 |
| 21 | 39333324973 |
| 22 | 336376244042 |
| 23 | 3029242658210 |
| 24 | 28439272956934 |
| 25 | 275986683743434 |
| 26 | 2789712466510289 |
| 27 | 29363495934315694 |
| (Sloane) |
We can now move on to a larger example.
An 8x8 Example:
We will solve the eight queens problem, but our solution method can be adapted to a board of any size;
Let us first look at an example solution:

figure 9: One of many solutions to 8-Queens problem.
In the example above there are eight queens on the board such that no queen threatens any other queen. There are 92 solutions in total. Let us find them all by writing a program to look for them. We will use recursion and backtracking.
Discussion
There are many kinds of techniques that can be used to find any one solution that will do better than backtracking through exhaustive search, but if we want to get all the solutions, there is no known algorithm that can do that efficiently. By efficiently as to mean in polynomial time in the number of the n-queens on n x n board.
Our goal is to get all the configurations.
The technique we are going to use is recursion with backtracking. Recursion is related to mathematical induction. Mathematical induction is outside the scope of this article, but you can learn more about it in any introduction book to algorithms. I highly recommend A Creative Approach to Algorithms by Udi Manber or The Algorithm Design Manual by Steven Skiena. Any book on algorithms would work. If you need a quick primer, check out Wikipedia entry on recursion.3
A short primer: a recursive solution to a problem has two kinds of statements. The first kind of statement solves the problem for the base case. A base case is a case where the answer to a problem is trivial, is known, or a logical statement that terminates the execution of a function (e.g. reached an end, a solved case, a special case, or a definition, etc.). This step is also called the terminating case—well because it terminates.
The second kind of statement, the recursive step is that which breaks a problem into smaller size of the previous problem or any step that brings a problem one step closer to completion. Remember if a recursive case diverges it will behave like an infinite loop. We are trying to slowly bring it closer to the base case.
The way we are going to be using recursion is to iterate through all the configurations. Our base case would be the case when we found a solution or exhausted our search space. That is when we have placed all eight queens in such a way that none of the eight queens threaten each other or there are no more configurations to try. The rest of the recursive solution would be picking a queen and placing it in such a way that it would not threaten any other queen and so on.
We also use backtracking as a way to record a series of previous steps such that we try all the configurations exactly once. This bookkeeping allows us to go back a step or two or three or N steps and try again. It allows for recovery and is a history of all our actions up to point t in time. Backtracking is useful for solving things like mazes or any problem where we would need to “back” up to our last known good state and to try another option. It is like leaving crumbs behind which can be used to trace back to the original location. With recursion it is a method to try every possible branch in a systematic way.
Backtracking records the queen placements. If the queen can be placed at a given cell (combination of row and column), we record it and try placing the next queen. If we get stuck going forward and run out of current choices, we use the information from our history to back up a step and try again with a different choice. We keep doing this until we have enumerated all the possibilities. Click here to see an existing trace of the technique above for a board size of 4x4. Here is another one for a board size of 8x8.
Representing the Board as a Matrix
We can represent the board as a two-dimensional matrix.

figure 10: One of many solutions to 8-Queens problem.
For example, the above board can be represented in the following matrix form:
$$\begin{pmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \end{pmatrix}$$
This representation makes it easy to visualize and check for queen conflicts as our representation mimics the graphical one. We can check for the queen conflicts by tracing each horizontal, vertical, and two diagonals such that no queen attacks another.
The pseudocode below shows how to check for conflicts if we place the queens starting from bottom left and place queens from left to right. We do not need to check for verticals because we only place one queen per vertical as we sweep across.
bool check(row, col) {
if ((row < 0 or row > N) and (col < 0 or col > N)) {
throw bad row
}
for(c = 0; c < col; c++)
if(board_[row][c])
return false;
for(r = row, c = col; r >= 0 and c >= 0; r--, c--)
if(board_[r][c])
return false;
for(r = row, c = col; r < N and c >= 0; r++, c--)
if(board_[r][c])
return false;
return true;
}
A more thorough check would be required if we would choose to populate the board randomly, using another method, or completing a partially populated board. Queens placement method allows for different optimizations.
void Solve(col) {
if(col >= N) {
record the solution
return; // solution found. done.
}
for(r = 0; r < N; r++) {
if(check(r,col)) {
board_[r][col] = true;
Solve (col+1);
board_[r][col] = false;
}
}
}
Call with Solve(0);
In the above pseudocode, we start with the left most coordinate (column zero or the x-coordinate) and check if the queen can be placed at that coordinate for each row (y-coordinate). We do the same in turn for all possible configurations for the next column and so on.
The board matrix acts as a history of our states up to column m. Before we call the function solve recursively for the next column (m+1), we store the queen at the valid location on the board and proceed. When m = N (max columns) we found a solution (the terminating case). At this point we can choose to stop looking at any more solutions if we just desire the one. Otherwise, the search will keep going until we run out of all possible combinations. To stop we would need to introduce a control variable and change the logic a bit.
Representing the Board as a Vector

figure 11: One of many solutions to 8-Queens problem.
It turns out that the chess board for this problem can also be represented using a vector. The way that works is as follows:
Let vector (array) v[x1 .. xn]={y1 .. yn} . Let x1 ..xn represent the columns and y1 ..yn represent the rows; let x[i]∈ N and y[i]∈ N where 0≤i<n .
Consider v={4,6,8,2,7,1,3,5}. Notice that the first element in v is the first queen in row 4. So v[queen’s column] = queen’s row. Think of a column as coordinate x and row as coordinate y. So v[x] = y.
A better way to check for queen conflicts
Note: The next technique for checking queen conflicts can also be used for the matrix representation of the board. We can also use the first technique to check for conflicts for the vector representation of the board.
We can efficiently check for queen conflicts. A bit of algebra and geometry would come in handy. We need to look closer at the horizontals and the diagonals and count them. We also need to find a way to represent them. So where to start?
The biggest piece of information is the board size. The board size influences how many horizontals and diagonals are in an n x n board? Let us take a closer look.
A board of size n must have n horizontals. The question for diagonals is not so clear. I suggest trying a small example and growing the board size to see a pattern emerge. How many falling diagonals are there for 1x1, 2x2, 3x3, 4x4, and so on. Similarly how many for rising diagonals? How many in total together? Take the time to count. Really. Stop and fiddle a bit with pen and paper. I really suggest you do. When done, proceed.
Well, the number for falling diagonals are 1, 3, 5, 7, 9, and so on for board size 1x1,2x2,3x3,4x4,5x5. Repeat the same for the rising diagonals.
This pattern fits an equation: $y= 2n-1$. We have one for the falling diagonal and one for the rising diagonal. We can prove this equation by using induction, or we can look it up for the time being. The next part is to consider the problem geometrically. What is a horizontal? What is a diagonal? What if we think of them as lines? Maybe we can learn something about their properties which can aid us. More on that soon, but first, how would we use the information to help us find conflicts.
Suppose we found a way of labeling horizontals and diagonals such that we can identify them with distinct numbers. For example, if given some integer X, and do not worry how we get integer X for now, this integer X must uniquely identify a line X’. Furthermore, suppose a diagonal line X’ runs through some cells. If we found a systematic way of associating a diagonal with cells, we could go in reverse—that is given the coordinates $(p,q)$ determine on which diagonal the coordinates $(p,q)$ belong to? Fortunately, it turns out that this is possible.
For the horizontals, the answer is trivial. Represent the horizontal as an array of size N. Each element in the horizontal[0..n-1] represents a horizontal row. For example, horizontal[0] would represent the most bottom row, horizontal[1] the second most bottom row, and so on. A value in horizontal[0..n-1] can be zero or one: zero for empty, one for occupied by a queen. Also this horizontal can be seen by an equation y = c. That is not a coincidence.
We have to find a similar way of doing the same for the two diagonals. This one can be quite tricky. If you remember from school a slope intercept form of a line is defined by the equation $y = mx + b$ where m is the slope and b is the y-intercept. The diagonals have a slope of -1 for a falling diagonal and 1 for a rising diagonal; each diagonal has a different value of b. The standard form of a line is $Ax + Bx = C$ where A,B,C are constants.
Below are two diagrams that show how a queen attacks and graphically superimposes the above equations.

figure 12: Shows a single queen threatening the squares on the board (marked in red)
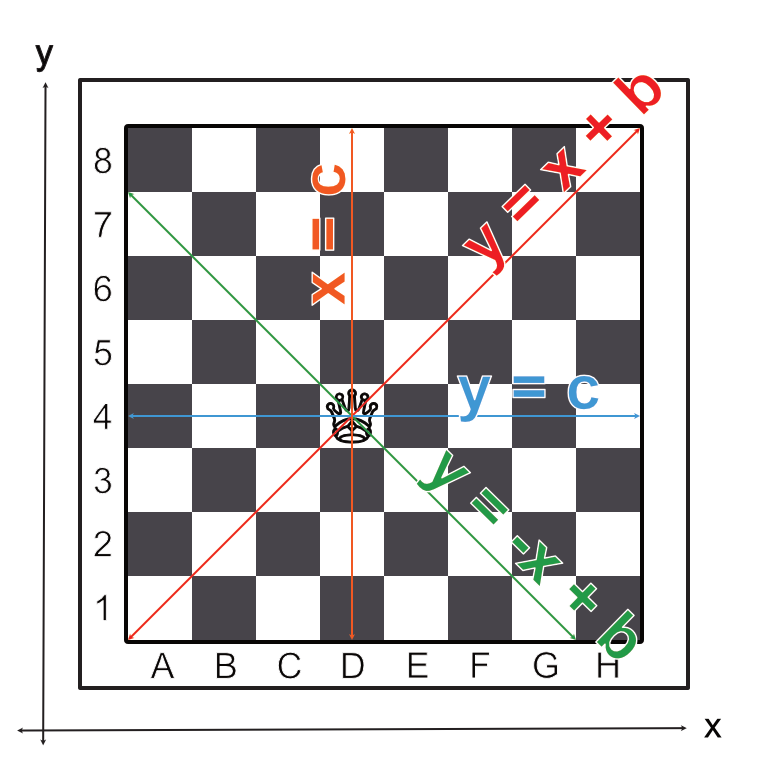
figure 13: Equations for attacking lines
If we arrange the equations in the diagram, we have: $y - x = b$ and $y + x = b$. We can use this to our advantage. (Eight Queens Problem, 2012)

figure 14: $y - x = b$

figure 15: $x + y = b$
If we graph all the equations, they look something like this:
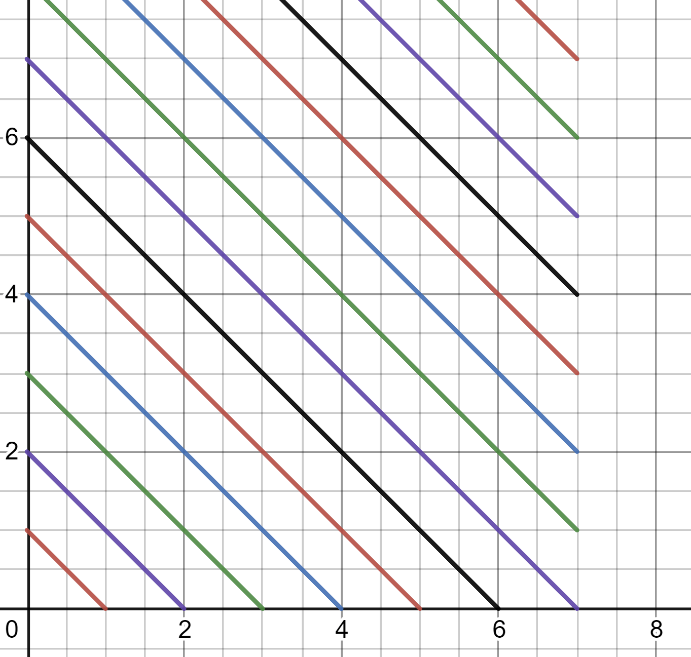
figure 16: falling diagonals
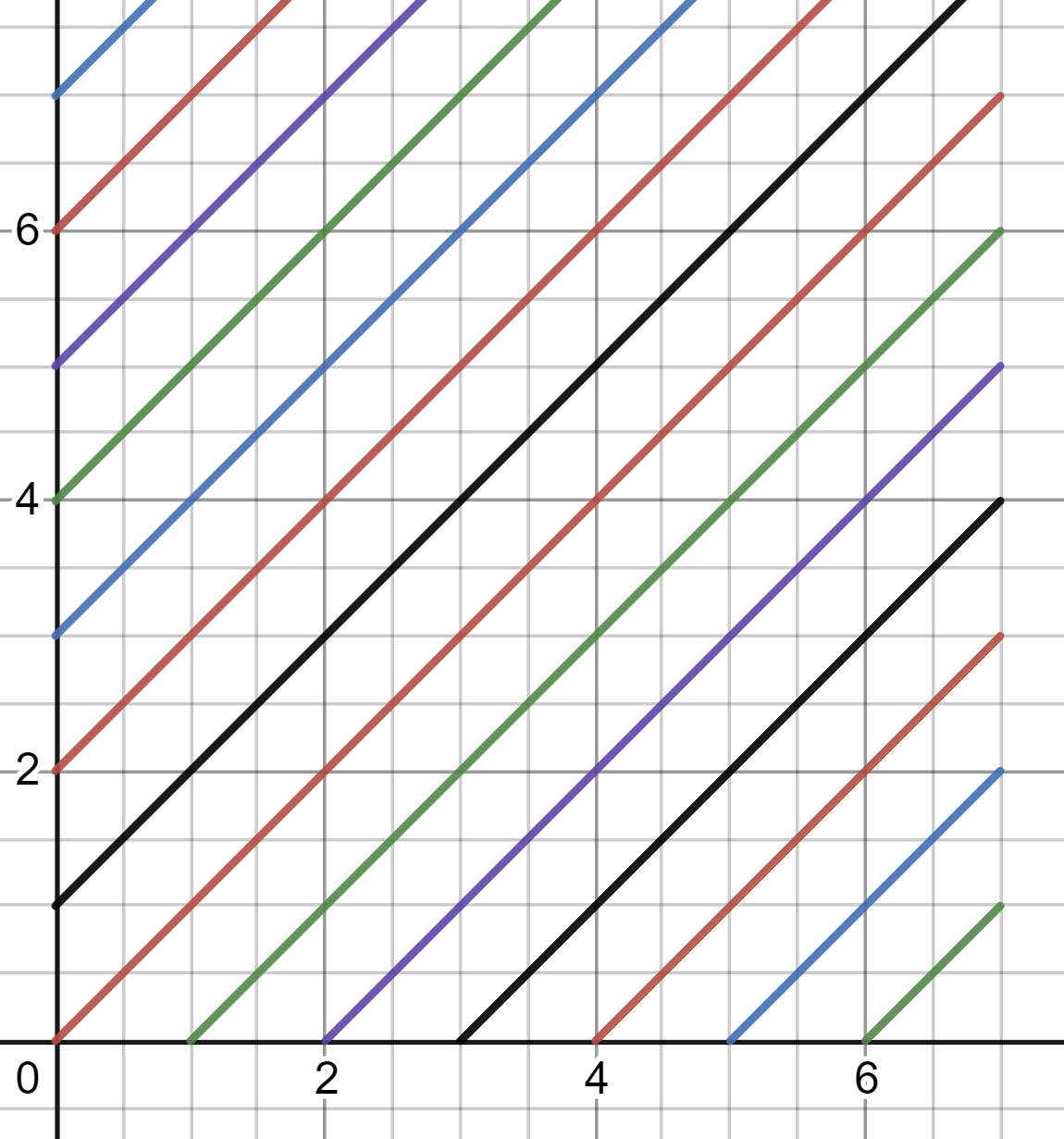
figure 17: rising diagonals
Now we overlay the diagonals with the sums:
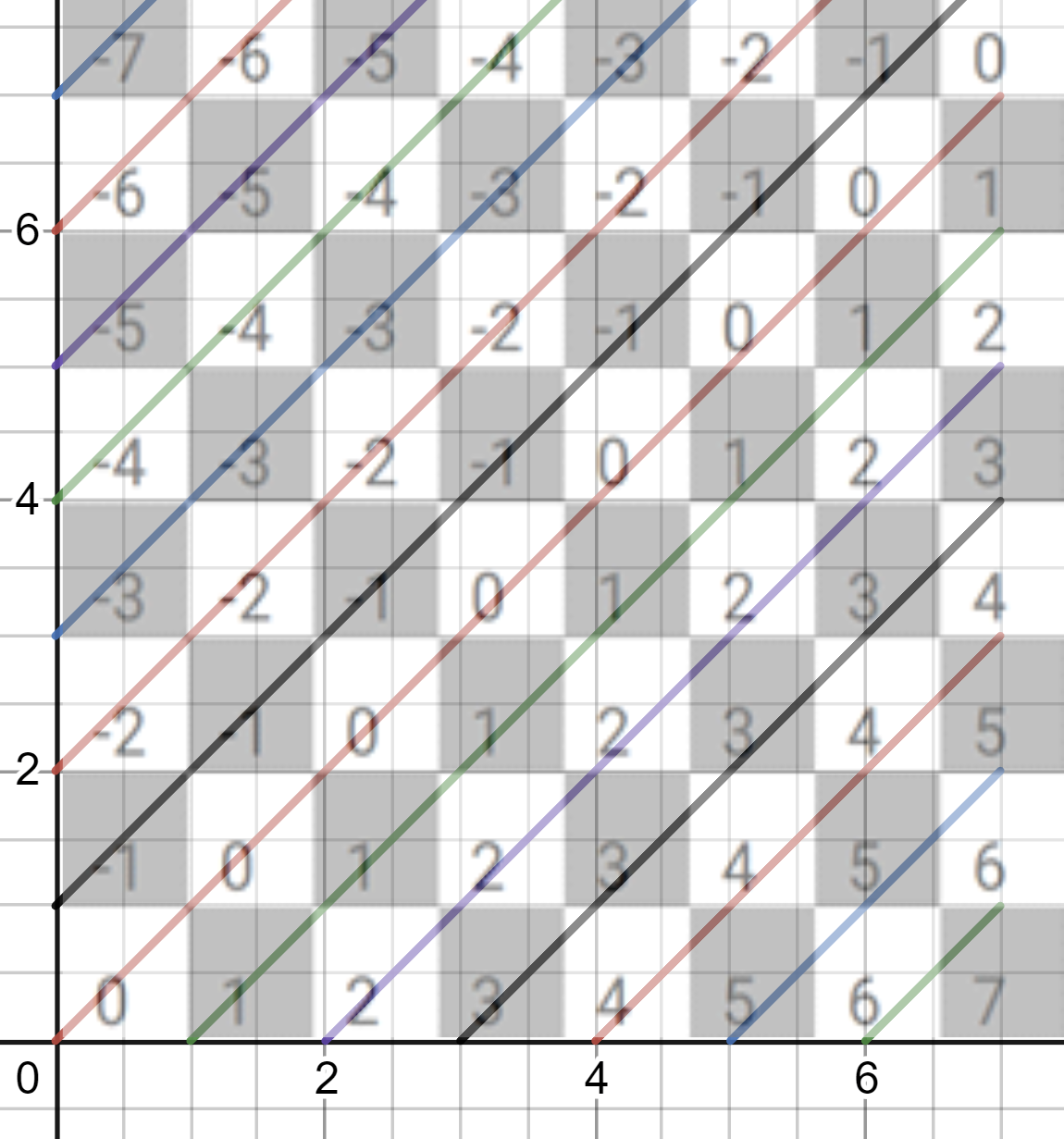
figure 18: overlay showing rising diagonals with $y - x = b$ where the value of $b$ is marked in the appropriate cell
Each diagonal has a value such that a distinct integer number represents the diagonal number. We can use this information to determine the diagonal for which the queen belongs in. This allows us to treat diagonals in the same way as horizontals.
Let us look at one more example. Consider the board above. Suppose we place a queen at $p_1(0,0)$. We cannot place any other queen where the number zero appears in the cells. Suppose we attempt to place a queen at $p_2(1,1)$. Can this be done? No! Why? For rising diagonals, the general line form is $x – y = C$. So, for $p_1$ we have 0-0 = 0 and for $p_2$ we have 1-1 = 0. This tells us that $p_1$(0,0) is on the same diagonal as $p_2(1,1)$.
bool good(x, y) {
return !horizotal[y] and !diaRise[y-x+n] and !diaFall[x+y];
}
This method allows us to determine, quickly, if the queen will conflict with another queen already placed. So three sets are sufficient: one for the horizontal and two for the diagonals. We do not need to account for the verticals; however, we can add a vertical set for completeness, but it is not necessary as long as, again, we place queens from left to right in a systamatic way. If that is not how we are placing the queens we would need a vertical set.
The solution below is very similar to the one using a matrix except we store the board in a vector and are able to check for queen conflicts. The logic is exactly the same as the previous algorithm.
void solve(x) {
if(x == n) {
a solution was found. Record it.
} else {
for(y = 0; y < n; y++) {
if(good(x,y)) {
board [x ] = y;
horizontal [y ] = true;
diaRise [y-x+n] = true;
diaFall [x+y ] = true;
solve(x+1);
board [x ] = NONE;
horizontal [y ] = false;
diaRise [y-x+n] = false;
diaFall [x+y ] = false;
}
}
}
}
Now that we have solved this problem it is time to reflect and ponder about what it all means. Problems like the n-queens problem are difficult problems for which there are no known efficient algorithms. Sometimes prohibitively expensive problems can be solved very quickly if the size is a small constant. We did that for the eight queens problem. One day larger boards can be fully solved in a few hours or minutes given faster hardware. But the general case of the n-queens problem will always elude us unless there is some major breakthrough in theory and understanding of such problems.
The technique we used is a general one: recursion with backtracking. This technique allows us to exhaustively enumerate every combination exactly once. We examined how to model our problem space. We also developed two methods to check for queen conflicts.
Notes
There seems to be a propagation error to whom the discovery of the problem should be attributed to. The exact source describing the historical error is: PAUL J. CAMPBELL, “GAUSS AND THE EIGHT QUEENS PROBLEM: A STUDY IN MINIATURE OF THE PROPAGATION OF HISTORICAL ERROR.” Succinctly, Paul Campbell mentions that Franz Nauck is not the one who originally proposed this problem but rather Max Bezzel two years prior. (Cambell, 1977)
Collections
A C++ Solution
A C++ solution is available here.
Another example of Recursion:
note: supporting content for recursion.
If recursion is new for you and seems confusing. Let us look at a simple problem.
A recursive function is like any other function except that it can call itself. For example, let us consider a simple factorial. Recall that a factorial is a function:
$f(n) = n! = n × (n -1) × (n-2) × … ×3 × 2 × 1$.
e.g., $4!= 4 ×3 ×2 ×1=24$. We can recursively define such a function: $n!= n ×(n-1)!$ , for all $n>1$ , where $0!=1$ and $1!=1$.
Pseudocode:
f(n) {
if (n == 0 or n == 1) {
return 1
}
return n * f(n-1)
}
So, a recursive execution trace of f(4) will look something like this:
f (4) = 4 * f(3)
= 4 * (3 * f(2))
= 4 * (3 * (2 * f(1)))
= 4 * (3 * (2 * 1))
= 4 * (3 * (2))
= 4 * (6)
= 24
References
Cambell, P. J. (1977). Gauss and The Eight Queens Problem: A Study in Miniature of the Propagation of Historical Error. Historia Mathematica, 397. Retrieved from http://langevin.univ-tln.fr/cours/PAA/tps/backtrack/histo-gauss.pdf
Eight Queens Problem. (2012, 01 07). Retrieved from Penn State Lehigh Valley: http://www2.lv.psu.edu/ojj/courses/cpp-lang/recursion/8-queens.html
Luria, Z. (2017). New bounds on the number of n-queens configurations. Retrieved from https://arxiv.org/abs/1705.05225
Sloane, N. J. (n.d.). Sequence A002562. Retrieved from The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.: https://oeis.org/A002562
Bibliography
Berry, N. (2012, 08 04). Eight Queens. Retrieved from DataGenetics: https://www.datagenetics.com/blog/august42012/
Clay Mathematics Institute. (2022, 01 18). The 8-Queens Puzzle. Retrieved 01 21, 2022, from Clay Mathematics Institute: http://claymath.org/events/news/8-queens-puzzle
Haran, B. (Director). (2015). The 8 Queens Problem - Numberphile [YouTube]. Retrieved from https://www.youtube.com/watch?v=jPcBU0Z2Hj8
Keevash, C. B. (2021). The n-queens problem. Retrieved from https://arxiv.org/abs/2109.08083v1
Simkin, M. (2021). The number of n-queens configurations. Retrieved from https://arxiv.org/abs/2107.13460v2
Sloman, L. (2021, 09 21). Mathematician Answers Chess Problem About Attacking Queens. Retrieved from Quantamagazine: https://www.quantamagazine.org/mathematician-answers-chess-problem-about-attacking-queens-20210921/
W.Dijkstra, E. (1971, 08). EWD316: A Short Introduction to the Art of Programming.
Wikipedia, Wikimedia Foundation. (2022, 01 20). P Versus NP problem. Retrieved from Wikipedia: https://en.wikipedia.org/wiki/P_versus_NP_problem
Wikipedia, Wikimedia Foundation. (2022, 01 18). Recursion. Retrieved from Wikipedia: https://en.wikipedia.org/wiki/Recursion_(computer_science)